Ramanujan’s lost notebook, q-series, and mock theta functions

St. Petersburg State University and Euler International Mathematical Institute are happy to announce a new advanced course, headed by Eric Mortenson. Lectures scheduled to Tuesdays starting 15 September, 7pm – 8:30pm. To attend the lectures, please join zoom channel 958-115-833. If you do not know the password, please write an email to Alina Zagorodnyuk <chebyshev.msc@gmail.com>. Video records of the course are available here.

Please note that there will be no lecture on 27 October. The last two lectures will then be 3 November and 10 November at the usual time.

Course description

Important variants of theta functions were discovered by the Indian mathematician Ramanujan in the early 20th century. Each mock theta function $f(q)$ was defined as a $q$ -series, convergent for $|q|<1$ , such that for every root of unity $\zeta$ , there is a theta function $\theta_{\zeta}(q)$ for which the difference $f(q)-\theta_{\zeta}(q)$ is bounded as $q\rightarrow \zeta$ radially; moreover, there is no single theta function which works for all $\zeta$ . Ramanujan’s third-order mock theta function $f(q)$ reads

$f(q):=\sum_{n\ge0}\frac{q^{n^2}}{(-q)_n^2}=1+\frac{q}{(1+q)^2}+\frac{q^4}{(1+q)^2(1+q^2)^2}+\dots$

Ramanujan stated identities relating mock theta functions to each other as well as to modular forms, which suggested that mock thetas live inside of a vector space, which has a subspace consisting of modular forms. Later, more identities were found in the Lost Notebook. Watson, Selberg, Andrews, and Freeman Dyson have worked on mock theta functions. Historically, mock theta functions have been studied under the settings of modularity and $q$ -hypergeometric series.

Zwegers answered how mock theta functions fit into modularity. He showed that Appell–Lerch functions, Fourier coefficients of meromorphic Jacobi forms, and special types of indefinite theta series all exhibit the same mock modular behaviour. Mock theta functions are holomorphic but not modular. To each mock theta function is associated a weight $3/2$ unary theta series called the shadow. By adding a non-holomorphic term determined by the shadow, a mock theta function may be completed to a function that is modular but no longer holomorphic. As a consequence, a mock theta function may be viewed as the holomorphic part of a weak harmonic Maass form after Bruinier and Funke.

Mock theta functions and their generalizations mock modular forms have been shown to play crucial roles in a variety of fields outside of number theory such as infinite-dimensional Lie superalgebras, Virasoro algebras, and conformal field theory, umbral moonshine, and black hole physics. In Ramanujan’s $q$ -series environment, one can construct objects that “leak” across the real-axis.

In this short course we hope to work through the following topics.

Overview of Ramanujan, 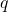$q$ -series, and mock theta functions.
Appell–Lerch functions, a heuristic, and Hecke-type double-sums; new Appell–Lerch function identities; and new proofs of classical mock theta function identities.
Kronecker-type identities and classical results on sums of squares and triangular numbers.
Threefield identities after Andrews, Dyson, and Hickerson; simultaneous representations of primes by binary quadratic forms; quantum modular forms.
Modular forms.
Mock modular forms.

Everyone is welcome!